低精度浮動小数点除算器に目処が立ってきたので、射影変換でもやってみようかと思いきや、もともとCGに余り慣れてないこともあって、射影変換の逆変換をする行列の作り方がわからず Maxima 使って解いてみたので備忘録程度に張っておきます。
solve([X=(a00*x+a01*y+a02)/(a20*x+a21*y+a22),Y=(a10*x+a11*y+a12)/(a20*x+a21*y+a22)],[x,y]);
に対する Maxima先生の解
[[x=(-a01*a22*Y+a02*a21*Y+(a11*a22-a12*a21)*X+a01*a12-a02*a11)/(-a00*a21*Y+a01*a20*Y+(a10*a21-a11*a20)*X+a00*a11-a01*a10),y=-(-a00*a22*Y+a02*a20*Y+(a10*a22-a12*a20)*X+a00*a12-a02*a10)/(-a00*a21*Y+a01*a20*Y+(a10*a21-a11*a20)*X+a00*a11-a01*a10)]]
えっと、斉次座標表現で書き起こすとこういうことかな?
(2017/09/09 ご指摘いただき、数式の表記ミスを修正しました)
ハードウェア作っていると、ソフトウェアと逆方向で座標計算したいケースも多いので、この辺の基礎は重要ですね。
メモリにWriteするときに変形するか、Readするときに変形するかによってやり方がいろいろ変わってきますね。
しかし、この手のツールが非常に賢くなってきて、手計算するのがどんどん億劫になっているので人間が変わりに退化していくような気も…



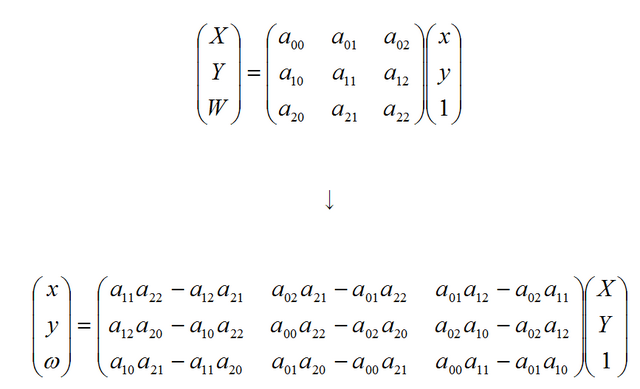


コメント