殆ど説明なく書き殴ってしまっているので一度整理しておく。
件の遊星歯車を使ったギアもOPアンプ回路もアナログ的には
A+B+C+D=0
A+D≦0
B+D≦0
-1≦A≦+1, -1≦B≦+1, -1≦C≦+1, -1≦D≦+1
という不等式を恒に満たす。
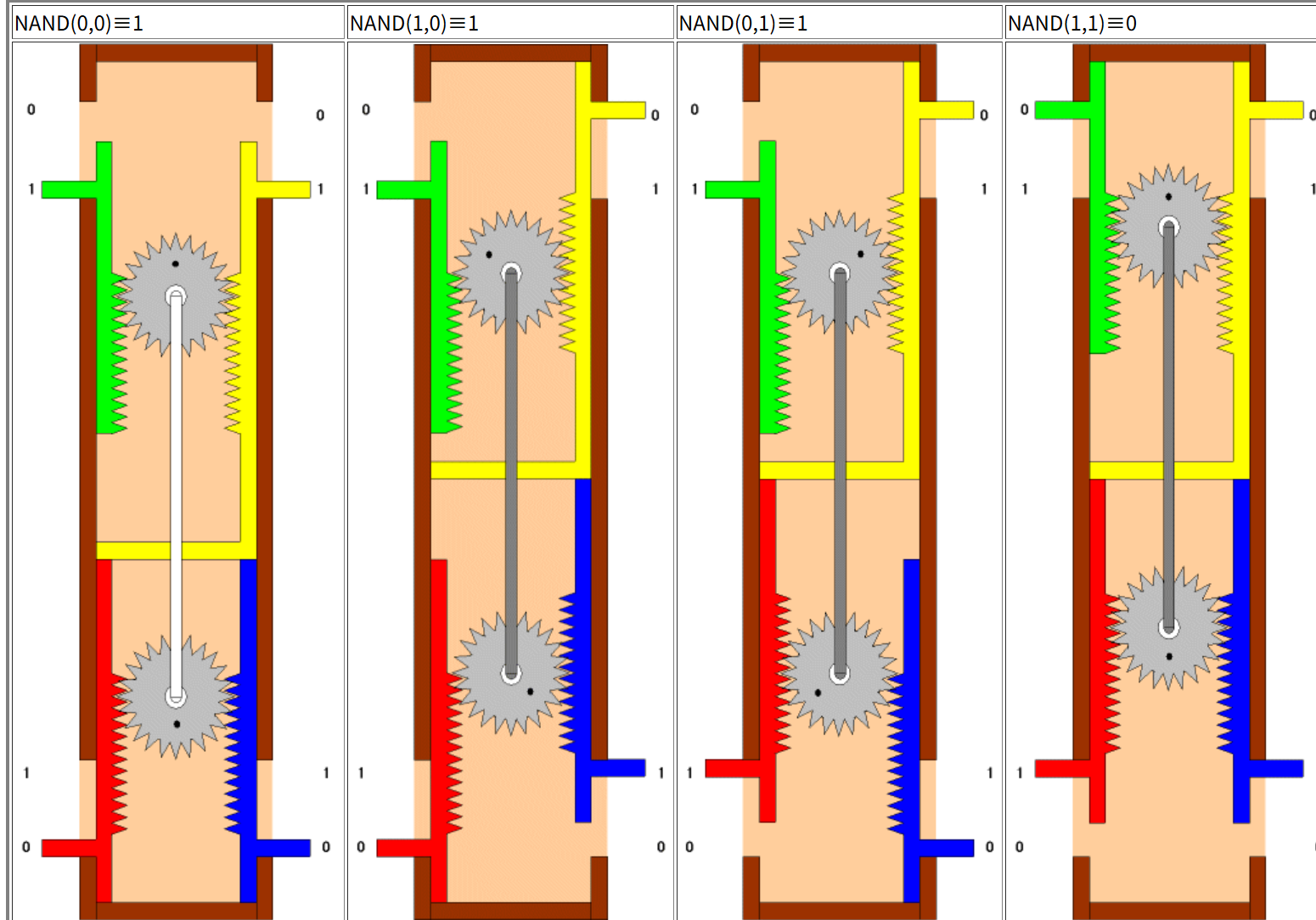
ここで一度デジタルな視点で、A~Cが 真(+1)、偽(-1) のどちらかの値しか取れないとすると論理式として
C = !(A・B)
という所謂NAND論理が成立する。
NAND論理がとり得る値の集合は
(A,B,C) = {(-1, -1, +1), (-1, +1, +1), (+1, -1, +1), (+1, +1, -1)}
の4パターンである。
ここで、再び初期の不等式でアナログ的に考えた場合、この4パターン間のそれぞれの遷移においてA,B,Cのうち何れかの値を固定したまま2値の連続変化による遷移が可能である。
即ちこのロジックの組合せで作った計算機械はデッドロックする恐れがない。
一方で、たとえばXORを数式で安直に表した場合
|A-B| – 2C = 0
という式が思いつく。
これには罠があり、
(A, B, C) = {(-1, -1, +1), (-1, +1, -1), (+1, -1, -1), (+1, +1, -1)}
の関係のうち
(-1, +1, -1) ⇔ (+1, -1, -1) の遷移で、Cを-1に固定したままABが入れ替わることが出来ない。
|A-B| – 2C = 0 を満たす回路は作成可能だが、もしこのような回路を作った場合、欲しい解に収束しない可能性がある。
では、先のNAND式の組合せでXORを作るとどうなるかであるが、ここで面白いことが起こる。
NAND式にはDという自由変数が組み込まれているが、これが所謂「遊び」となり、値間の遷移でポテンシャルの壁を作らない。変わりにA,B,Cは A≦0 とかの領域としての束縛のみを受ける。この領域がデジタル的な解を限定しつつも、恒常的に凸多角形を壊さないため局解にデッドロックすることなく計算が進行する。



コメント